Introduction and Overview
3D surveys have evolved a great deal in the past two decades. We have become keenly aware of the importance of offset and azimuth distributions, wide aperture patches, pre-stack migrations and so forth. However, there remains a misguided perception that the regularity of design must be maintained and that statistics of specific bins within a 3D bear significant impact on the quality of the final processed image.
This manner of thinking has led a large sector of geophysicists to believe strongly in the 3D acquisition geometry known as the "Brick" (named because the resemblance of the geometry plot to a brick wall). In this discussion, I wish to draw the reader's attention to a broader statistical evaluation of the brick pattern and show why I believe it is technically inferior to some other designs. I will also point out the obvious operational inefficiencies of the brick pattern.
Consider the regular grid of orthogonal source and receiver lines in the following figure. Each subsurface bin will contain midpoints of many source-receiver pairs. Within each bin, we can describe the offset and azimuth distribution as well as the conventional fold diagram.
We refer to this model as a "Sparse" 3D (as opposed to a fully sampled 3D).

|
A full wave-field sampled 3D grid would require a receiver line separation equal to the source interval and a source line separation equal to the receiver interval. In other words, for 30 m x 30 m natural bins, we would use source and receiver intervals of 60 meters. For full wave-field sampling, we would require lines of sources with sources separated by 60 m and lines every 60 m. Every 60 m by 60 m surface bin would contain a source point. This would provide full sampling in the source domain. Similarly, full sampling in the receiver domain would require a receiver in every 60 m x 60 m surface bin.
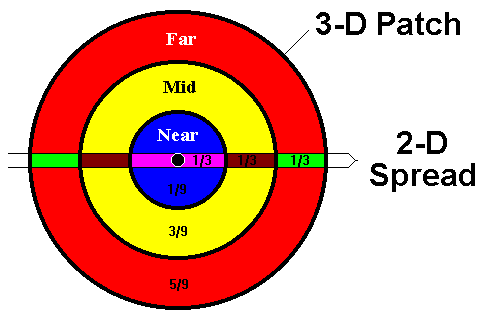
Such a fully sampled 3D would be very expensive, but it would provide uniform offset statistics in every bin. In each and every bin, we would record at least one trace from every offset position available within our patch. The "Mega-Bin" style of recording developed by PanCanadian Petroleums (Bill Goodway and Brent Ragan), is a reasonable approximation to the fully sampled model.
Often, we allow our designs to be driven by desired fold rather than full offset sampling. For targets where offsets longer than about 700 meters are useful, this will generally yield a fairly sparse line spacing compared to the "Mega-Bin" style.
For fully sampled 3D's:
|
For "MegaBin" 3D's:
|
| For conventional "Sparse" 3D's:
|
Such surveys will always yield some degree of bin-to-bin heterogeneity. That is, not every bin will contain traces from all offsets. Furthermore, the offset sampling will vary from one bin to the next.
It is this statistical heterogeneity that concerns geophysicists. It interferes with wavelet stability, multiple suppression and AVO analysis.
Regular Orthogonal Grid
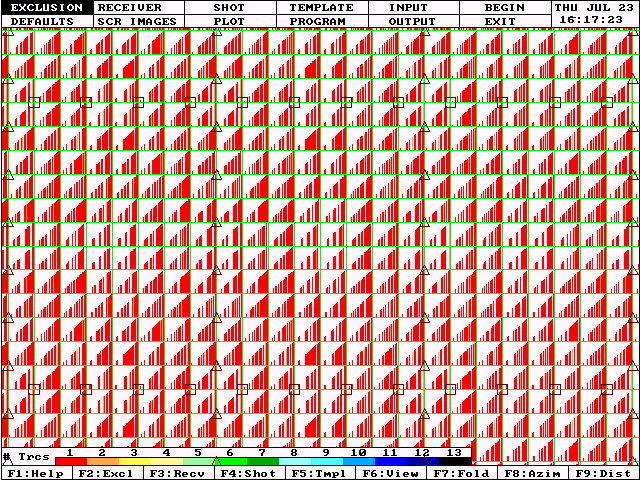
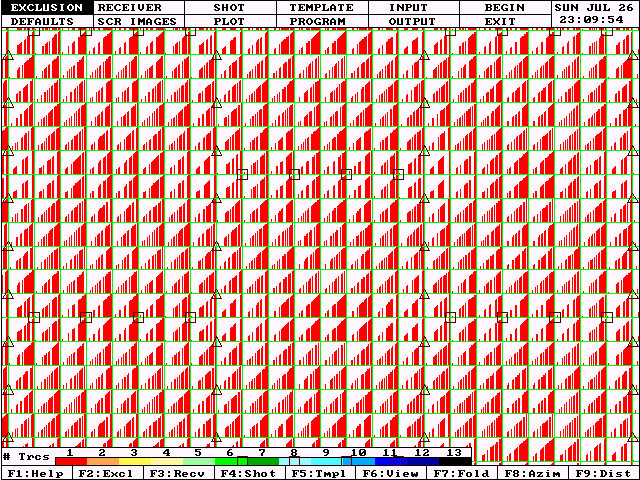
The following diagram is a typical representation of the offset distribution of a regular orthogonal grid design. We have zoomed in on a small area near the center of a large survey. Receiver groups are represented by triangles, source points by squares. We will refer to the area bounded by two adjacent source lines and two adjacent receiver lines as a "box". Notice that this zoomed display shows three complete boxes.
Also notice that this is a mildly sparse 3D in that the receiver lines are separated by 4 source intervals and the source lines are separated by 6 receiver intervals. (We are recording every 4th receiver line and every 6th source line of a fully sampled model.) The source and receiver intervals are 60 meters (yielding natural bins 30 m x 30 m). The source lines are 360 m apart and the receiver lines are 240 m apart. This survey is designed to produce a nominal fold of about 2000% (20 fold) assuming source-receiver offsets from 0 to 1500 meters are useable and a wide aperture recording patch is used.
Due to bin heterogeneity and geometric imprinting, the actual redundancy in each bin will vary from 19 to 22 fold within the full fold area. But far more important than the count of traces contributing to each bin is the variety of source-receiver offsets represented.
|
Our subsurface bin size is 30 meters. Therefore, in the offset range from 0 to 1500 meters, we could expect 1500 / 30 = 50 unique offset positions. Since we only have about 20 traces per bin, we obviously cannot observe every unique offset position in every bin (only about 20 fold / 50 possible offset positions = 40%). Hence, the result is offset heterogeneity within each box of our survey. This heterogeneity becomes more severe as the sparseness of our design increases.
We also recognize that wide aperture 3D recording results in an offset distribution that favors far offsets. In the above model, more than 50% of our traces will be generated by offsets from 1000 to 1500 meters and less than 10% will have offsets from 0 to 500 meters.
|
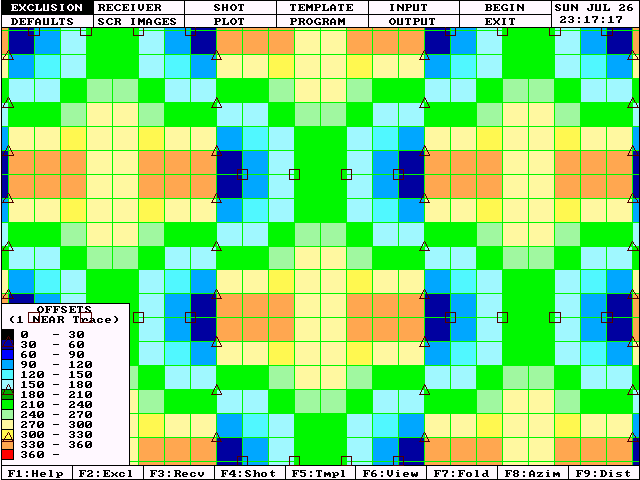
Close examination of Figure 2 reveals that almost all bins sample the far offsets quite well. However, some bins are deficient in near offsets (particularly near the center of each box). Furthermore, some bins are represented by a fairly uniform distribution of offsets while others exhibit a "clumpy" distribution. We wish to minimize this clumpiness and develop models with smooth distributions of offsets (actually offset2) in all bins.
In the regular orthogonal grid design, the bin at the center of each box is handicapped in near offsets. The nearest source-receiver pairs with a mid-point in the central bin of each box will be those with a source near one corner of the box and a receiver near the diagonally opposite corner of the box. Therefore, the box diagonal limits the nearest offset contributing to the bins at the box centers.
The following diagram uses color coding to reflect the nearest offset available in each bin. Note that near offsets are readily available in the bins near line intersections, but bins near the box centers are more limited in near offsets.
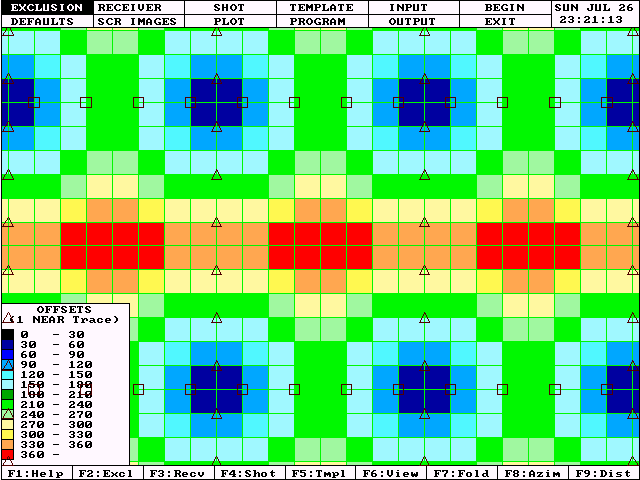
|
It is this phenomenon that prompted the concept of the "Brick" pattern for 3D programs.
Double and Triple Brick Patterns
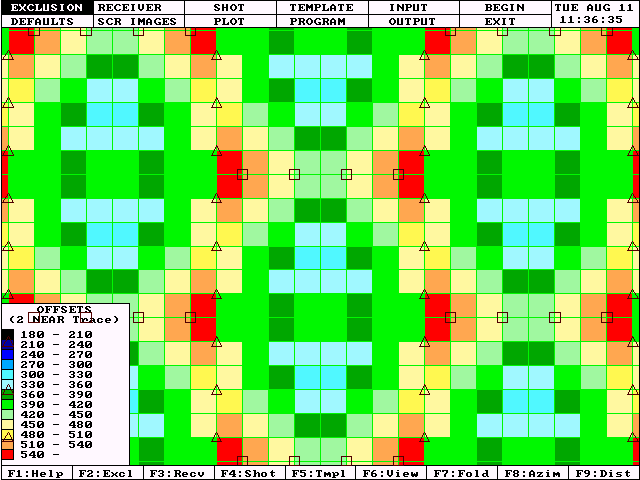
Figure 5 shows a detail of the offset distribution achieved by a double brick design. Notice that the source lines (sources are represented by squares) are not continuous. Each salvo of sources is offset by one half of the source line spacing.
|
Compare the nearest offset trace contributing to the central bin of each box to the corresponding traces in the regular grid model (Figure 2). It certainly appears as though the brick model generates a nearer offset contribution to the central bins than the regular grid model. The nearest offset analysis in Figure 6 confirms this conclusion.
|
This simple observation has led many geophysicists to conclude that the brick pattern provides a superior offset distribution to the regular grid. Unfortunately, this conclusion is based on observing only the characteristics of the nearest offset trace in each bin.
Examine Figure 5 once again. This time, focus on the columns of bins underlying the receiver lines (triangles). Notice that each bin contains a very near offset trace. But, for many of these bins, the next nearest contribution is a mid-offset. There is a large gap from the one nearest trace to the second nearest trace. This deficiency tends to form a linear alignment along the receiver lines with the worst occurrences near intersections with source salvos.
I have often heard geophysicists state, rather casually, that "brick patterns add more near offsets". Since we are recording the same number of receivers and shooting the same number of source points, we cannot be "adding" any traces to our survey. If we observe a near offset in one bin, it must be because we have removed that offset from some other bin.
|
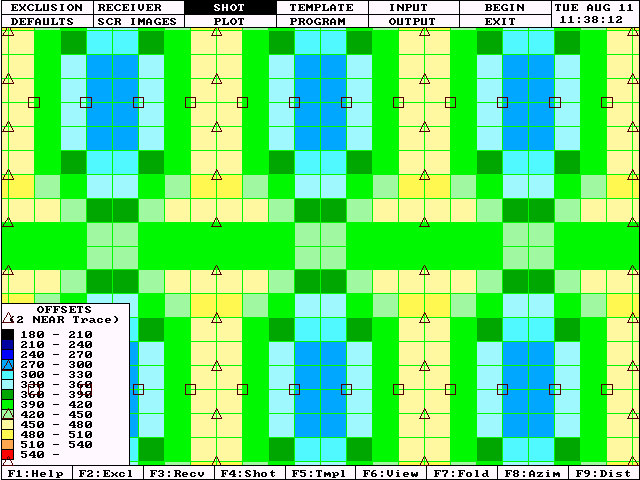
Figures 7 and 8 clearly show the superiority of the regular offset grid over the double brick pattern if we use the second nearest offset contribution in each bin as a measure of quality.
This display of the offset of the second nearest trace in each bin shows that the worst case second offset exceeds 540 m and that 16 bins in each box are the same as, or longer than the worst bins in the previous example. Note the linear alignment of the deficient bins under the receiver lines. |
If we are going to re-arrange offset distributions, we should ensure that we are not creating deficiencies in unexpected areas. We must examine more than just the nearest offset contributions to each bin. We should select the grid geometry that provides the least disruptive patterns. Most interpreters will agree that linear alignments of statistical artifacts in a 3D survey are more harmful than "blotchy" or "patchy" areas of deficiency.
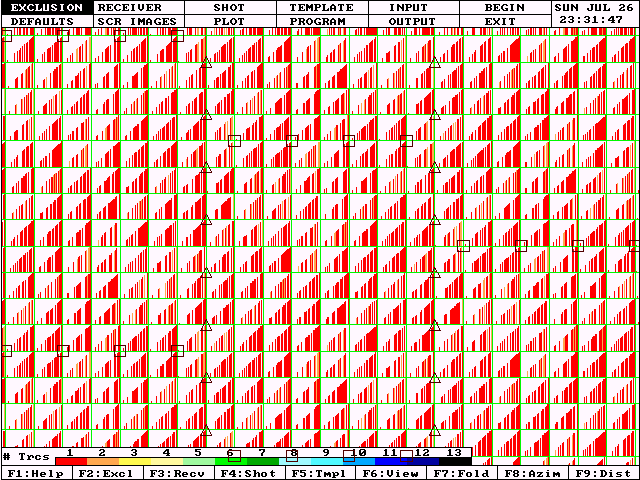
|
The "triple brick" pattern represented in Figure 9 is an improvement over the double brick. But we still see many bins under the receiver lines that are deficient in near offsets (except for the one nearest trace). The extent of the linearity of this deficiency is reduced.
To study the distribution of the nearest offset or the second nearest offset or any other single trace is folly. The quality of our stacked trace depends on many statistics of all traces contributing to each bin (offset uniformity, azimuth sampling, fold). The trace to trace stability of our final data volume depends on the uniformity of these statistics.
The brick patterns are not better than more conventional orthogonal designs when all statistics are examined. The statistical footprints of the brick pattern may be more detrimental to our final interpretations.
Certainly, it is not disputed that the brick provides more challenges in field implementation. In bushy areas, where line of sight is limited to cut trails, and where GPS surveying may not be practical, the brick pattern forces many more turning points for surveyors. Setting out liners for line-of-sight cutting requires full time attendance of a surveyor with the cutting crew. Traversing source lines with heavy equipment such as tandem drills or vibrators requires a great amount of detouring along receiver lines. In heli-portable programs, it is very difficult to follow source lines from the air. In sensitive permit areas, access payments increase dramatically.
All such operational detriments have been overlooked because the brick was touted as a technically superior design. Certainly, technical merit justifies some increase in field effort. However, I strongly believe that the brick pattern lacks technical merit. In fact, it is probably technically detrimental.
For a technique that lacks technical merit, and introduces additional complications to field implementation, the brick has gained wide spread use. As best as I've been able to determine, this has been due to misguided emphasis on a small subset of quality measures of a 3D design strategy. It has also been a case of many sheep following a few leaders.
The Diagonal Model
One outgrowth of the triple brick is the "Diagonal" grid. Figure 10 shows the offset distribution for one type of diagonal grid. In this case, each source lies west of the previous source by one source interval and north by a half a source interval. This results in the same total number of sources and receivers as the previously discussed surveys, but will require about 12% more linear kilometers of source line. This may be significant in areas where cutting and line preparation costs are high.
The nearest offset distribution is as good as the brick patterns and better than the offset orthogonal grid. The second nearest offset is not much better than the bricks and inferior to the offset orthogonal.
Statistical redundancies and symmetries are reduced using the diagonal grid. The "box" is distorted from a rectangle to a parallelogram. Note that the offset across one diagonal of the box is no longer redundant with the offset across the other diagonal.
Diagonal grids can often make better use of existing trails in wooded areas. It is not often that we see a good set of orthogonal trails already cut. More often, we see a variety of azimuths of existing trails. Diagonal grids can often be designed to optimize the use of such trails.
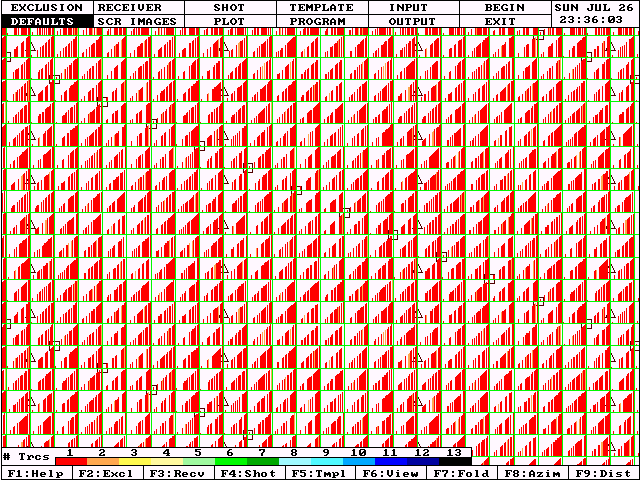
|
Summary
Any 3D design that does not provide full wave-field sampling will introduce bin-to-bin heterogeneity in key statistics. Fold, offset and azimuth distributions will be under sampled and irregular. It has been professed that brick patterns provide "better" distributions of offsets. This conclusion is based an analysis of only the nearest trace in each bin. In fact, deficiencies in other offset ranges form stronger patterns in brick designs than regular orthogonal designs.
Mustagh Resources Ltd. is developing software to analyze the standard deviation of differences in ordered squared offsets within each bin in an attempt to better understand the "clumpiness" of offset distributions. We hope this will provide a more meaningful evaluation of the quality of different design strategies. (Monitor our web page for updates on this analysis and for upcoming papers on random 3D's and skid and offset principles.)
Some designs promise improved statistics but are difficult to implement. Often the technical merit of these designs is not robust under perturbation. That is, if many points must be offset in the field (if we are unable to locate source points at all modeled locations), then the technical quality of the model seriously deteriorates.
We believe that the measure of quality of one model versus another must evaluate not only the complete impact on all statistical measures, but also the integrity of the model after reasonable perturbation. Will the model quality survive the reality of implementation in a difficult environment?
Under these measures, the brick patterns are significantly inferior to offset orthogonal grids and diagonal grids. Furthermore, the diagonal grid may be inferior to the offset orthogonal design, although we reserve judgement on this until we finish our analysis software.
Certainly, it is important to understand the effects of perturbation on these models. It is of utmost importance to clearly establish criteria for acceptable perturbation. These criteria will form the basis of skid and offset guidelines. Mustagh Resources Ltd. has completed significant studies on these topics and we will soon be offering another paper on our web page addressing this issue.
For now, we encourage all our clients to avoid the brick patterns in 3D design. We have established skid and offset guidelines designed to maintain the most desirable statistical distributions subject to anticipated actual field perturbations. Beware of evaluations of design patterns that focus on the statistics of individual traces or specific bin within a program. Our objective is to provide high quality traces throughout the 3D volume. Each stacked trace is influenced by the offset and azimuth statistics of all contributing traces.
Norman M. Cooper, P.Geoph.